Géométrie : Minoration d'un périmètre
2 participants
Page 1 sur 1
 Géométrie : Minoration d'un périmètre
Géométrie : Minoration d'un périmètre
Soit le triangle `ABC` avec `A(a,0)`, `B(0,b)`, `C(c,d)` dans un repère orthonormé et `a, b, c, d > 0`. Montrer que le périmètre de ce triangle est `>=2 *CO` (où O est l'origine du repère).
 Re: Géométrie : Minoration d'un périmètre
Re: Géométrie : Minoration d'un périmètre
Si C se retrouve à l' intérieur du triangle OAB, alors la propriété est évidente!

Si C appartient au segment `[AB]`, alors le périmètre du triangle vaut deux fois la distance AB, qui est plus grand que la distance de l' origine jusqu' à quelque point du segement `[AB]`.

Si on fait tendre A et B vers 0, alors le périmètre devient deux fois la distance OC.
Si on ne fait que tendre que A ou B vers 0, alors on a que le triangle ABC devient le triangle OAC par exemple. Dans ce cas il suffit de montrer que `OC<=OA+AC`. Or dans un triangle non-plat, cette propriété est évidente!

Soit M le milieu de [AB]:
Si C appartient à (OM):
`OM=AM=AB` et `OC=OM+MC
donc `2*OC=2*(OM+MC)=AM+MB+2MC=AB+2MC
dans ce cas il suffit de montrer que `2MC<=BC+AC
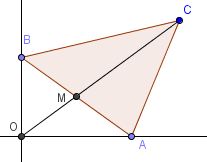
Si C se trouve à proximité de M, alors on peut facilement voir que la propriété est vérifiée.
`2MC<=BC+AC
Or MC est la médiane de C du triangle ABC et AC et BC sont les côtés "ajacents" à cette médiane.
Or la formule dite de la médiane dit que:
`4MC^2+AB^2=2BC^2+2AC^2
`iff2MC=sqrt(2BC^2+2AC^2-AB^2)
Je continuerai bientôt, je dois encore un peu réfléchir , je ne sais pas trop comment le faire...

Si C appartient au segment `[AB]`, alors le périmètre du triangle vaut deux fois la distance AB, qui est plus grand que la distance de l' origine jusqu' à quelque point du segement `[AB]`.

Si on fait tendre A et B vers 0, alors le périmètre devient deux fois la distance OC.
Si on ne fait que tendre que A ou B vers 0, alors on a que le triangle ABC devient le triangle OAC par exemple. Dans ce cas il suffit de montrer que `OC<=OA+AC`. Or dans un triangle non-plat, cette propriété est évidente!

Soit M le milieu de [AB]:
Si C appartient à (OM):
`OM=AM=AB` et `OC=OM+MC
donc `2*OC=2*(OM+MC)=AM+MB+2MC=AB+2MC
dans ce cas il suffit de montrer que `2MC<=BC+AC

Si C se trouve à proximité de M, alors on peut facilement voir que la propriété est vérifiée.
`2MC<=BC+AC
Or MC est la médiane de C du triangle ABC et AC et BC sont les côtés "ajacents" à cette médiane.
Or la formule dite de la médiane dit que:
`4MC^2+AB^2=2BC^2+2AC^2
`iff2MC=sqrt(2BC^2+2AC^2-AB^2)
Je continuerai bientôt, je dois encore un peu réfléchir , je ne sais pas trop comment le faire...

carole- Expert

- Messages : 181
Date d'inscription : 11/05/2010
Age : 31
 Trop de cas ...
Trop de cas ...
On peut faire l'exercice avec un raisonnement universel, c-à-d qui marche dans tous les cas 
Je te laisse encore réfléchir un peu ...
Cordialement, G. Lorang
Je te laisse encore réfléchir un peu ...
Cordialement, G. Lorang
 Solution
Solution
On place sur la figure le point `D` tel que `ACBD` est un parallélogramme et le milieu `M` de [AB].
D'après l'inégalité triangulaire :
`OC<=OM+MC`
`iff 2OC<=2OM+2MC`
Or :
1) Le triangle `OAB` est rectangle en `O`, donc `2OM=AB` (diamètre du cercle circonscrit)
2) `2MC=CD` est la diagonale du parallélogramme et d'après l'inégalité triangulaire : `CD<=CA+AD=CA+BC`
Donc : `2OC<=AB+AC+BC`
Cordialement, G. Lorang
D'après l'inégalité triangulaire :
`OC<=OM+MC`
`iff 2OC<=2OM+2MC`
Or :
1) Le triangle `OAB` est rectangle en `O`, donc `2OM=AB` (diamètre du cercle circonscrit)
2) `2MC=CD` est la diagonale du parallélogramme et d'après l'inégalité triangulaire : `CD<=CA+AD=CA+BC`
Donc : `2OC<=AB+AC+BC`
Cordialement, G. Lorang
 Sujets similaires
Sujets similaires» Géométrie : Aire délimitée par 3 cercles
» Géométrie dans l'espace : Calcul d'un angle
» Géométrie : Aire d'un disque inscrit (OMB Maxi)
» Géométrie : Une fonction identiquement nulle définie sur le plan
» Théorème de Leibniz
» Géométrie dans l'espace : Calcul d'un angle
» Géométrie : Aire d'un disque inscrit (OMB Maxi)
» Géométrie : Une fonction identiquement nulle définie sur le plan
» Théorème de Leibniz
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum|
|
|
