OMB Eliminatoires 2013
3 participants
Page 1 sur 2
Page 1 sur 2 • 1, 2 
 OMB Eliminatoires 2013
OMB Eliminatoires 2013
Voici le questionnaire MIDI des épreuves éliminatoires de l'OMB de cette année:
(Le questionnaire se trouve à cette adresse:
http://omb.sbpm.be/modules/eli/eli.php?id=21424 )
1.

2.
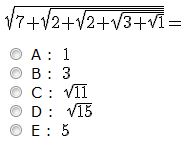
3.
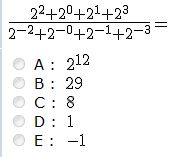
4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.
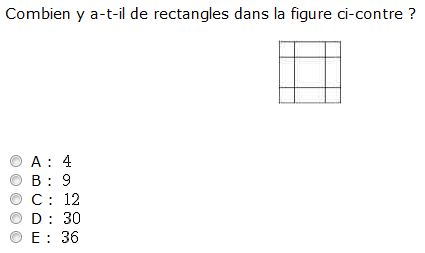
24.

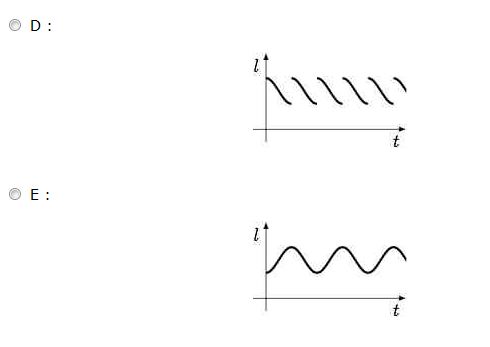
25.

26.

27.

28.

29.

30.

(Le questionnaire se trouve à cette adresse:
http://omb.sbpm.be/modules/eli/eli.php?id=21424 )
1.

2.
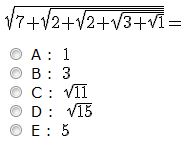
3.
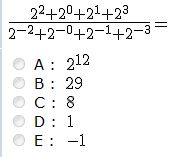
4.

5.

6.

7.

8.

9.

10.

11.

12.

13.

14.

15.

16.

17.

18.

19.

20.

21.

22.

23.

24.


25.

26.

27.

28.

29.

30.


carole- Expert

- Messages : 181
Date d'inscription : 11/05/2010
Age : 31
 Réponses
Réponses
1) D 2) B 3) C 4) D 5) E 6) C 7) D 8) B 9) B 10) 631
11) D 12) B 13) 119 14) 120 15) E 16) C 17) A 18) C 19) C 20) C
21) E 22) E 23) E 24) B 25) 72 26) C 27) A 28) E 29) E 30) A
11) D 12) B 13) 119 14) 120 15) E 16) C 17) A 18) C 19) C 20) C
21) E 22) E 23) E 24) B 25) 72 26) C 27) A 28) E 29) E 30) A
 Question 30
Question 30
On peut recouvrir le rectangle 6x1 de 13 façons différentes avec des rectangles 2x1 et 1x1:

Donc la réponse A) est correcte.

Donc la réponse A) est correcte.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Question 29
Question 29
Prenons l'exemple d'un homme pesant 64 kg et ayant une taille de 1,80 mètres. Son BMI est donc de 19,753. Si la nouvelle taille de la personne est de 1,90 mètres alors:
`19,753(kg)/m^2=m/(1,90m)^2`
`iff m=71,309 kg`
Donc la personne pèse 7,309 kg plus qu'avant. Donc on peut supposer que E) soit la bonne réponse. Et en effet, si une personne de même masse et de 1,70 m (BMI=22,145) grandit de 10 cm:
`22,145(kg)/m^2=m_2/(1,80m)^2`
`iff m_2=71,751 kg`
Donc la masse de cette personne dépend de la taille initiale.
`19,753(kg)/m^2=m/(1,90m)^2`
`iff m=71,309 kg`
Donc la personne pèse 7,309 kg plus qu'avant. Donc on peut supposer que E) soit la bonne réponse. Et en effet, si une personne de même masse et de 1,70 m (BMI=22,145) grandit de 10 cm:
`22,145(kg)/m^2=m_2/(1,80m)^2`
`iff m_2=71,751 kg`
Donc la masse de cette personne dépend de la taille initiale.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Question 28
Question 28
Déterminons d'abord les coordonnées des sommets du triangle.
Soit `A(x_A;y_A)` tel que:
`{(y_A=0),(y_A=x_A):}`
`B(x_B;y_B)` tel que:
`{(y_B=x_B),(y_B=-2x_B+21):}`
Et `C(x_C;y_C)` tel que:
`{(y_C=0),(y_C=-2x_C+21):}`
Après avoir résolu ces systèmes, on trouve `A(0;0)`, `B(7;7)` et `C(21/2;0)`.
Soit `H` le point où la hauteur issue de `B` coupe `(AC)`. Pour trouver les coordonnées de `H`, il faut trouver l'équation de la droite (BH). Comme la pente de celle-ci tend vers l'infini (elle est perpendiculaire à `(AC)` dont la pente est 0), il suffit de déterminer `x_H`. Or, `x_H` doit être égal à `x_B`, donc `H` a les coordonnées `H(7;0)`.
`Aire(ABC)=(AC*BH)/2
Il est évident que `AC=21/2` et `BH=7`, alors:
`Aire(ABC)=((21/2)*7)/2
`=36,75`
Réponse E) est correcte.
Soit `A(x_A;y_A)` tel que:
`{(y_A=0),(y_A=x_A):}`
`B(x_B;y_B)` tel que:
`{(y_B=x_B),(y_B=-2x_B+21):}`
Et `C(x_C;y_C)` tel que:
`{(y_C=0),(y_C=-2x_C+21):}`
Après avoir résolu ces systèmes, on trouve `A(0;0)`, `B(7;7)` et `C(21/2;0)`.
Soit `H` le point où la hauteur issue de `B` coupe `(AC)`. Pour trouver les coordonnées de `H`, il faut trouver l'équation de la droite (BH). Comme la pente de celle-ci tend vers l'infini (elle est perpendiculaire à `(AC)` dont la pente est 0), il suffit de déterminer `x_H`. Or, `x_H` doit être égal à `x_B`, donc `H` a les coordonnées `H(7;0)`.
`Aire(ABC)=(AC*BH)/2
Il est évident que `AC=21/2` et `BH=7`, alors:
`Aire(ABC)=((21/2)*7)/2
`=36,75`
Réponse E) est correcte.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Question 27
Question 27
`(x-1)^4-(x+1)^4=0`
`iff ((x-1)^2-(x+1)^2)((x+1)^2+(x-1)^2)=0`
`iff (x-1)^2=(x+1)^2` ou `(x+1)^2=-(x-1)^2`
`iff x^2-2x+1=x^2+2x+1` ou `x^2-2x+1=-x^2-2x-1`
`iff -4x=0` ou `2x^2+2=0`
`iff x=0`
La somme de des solutions est égal à 0. A) est correct.
`iff ((x-1)^2-(x+1)^2)((x+1)^2+(x-1)^2)=0`
`iff (x-1)^2=(x+1)^2` ou `(x+1)^2=-(x-1)^2`
`iff x^2-2x+1=x^2+2x+1` ou `x^2-2x+1=-x^2-2x-1`
`iff -4x=0` ou `2x^2+2=0`
`iff x=0`
La somme de des solutions est égal à 0. A) est correct.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Question 26
Question 26
Calculons d'abord l'aire de ABC. Comme `AB=3` et `AC=4`, l'aire vaut:
`(AB*AC)/2` (car `ABC` est rectangle en A)
`=(3*4)/2=6`
Comme le triangle formé par les milieux d'un triangle est 4 fois plus petit que l'autre, l'aire de `XYZ` est le quadruple de celui de `ABC` qui est égal à 24. Ainsi la réponse C) est correcte.
`(AB*AC)/2` (car `ABC` est rectangle en A)
`=(3*4)/2=6`
Comme le triangle formé par les milieux d'un triangle est 4 fois plus petit que l'autre, l'aire de `XYZ` est le quadruple de celui de `ABC` qui est égal à 24. Ainsi la réponse C) est correcte.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Question 25
Question 25
Soit `t` la longueur de la tête, `c` la longueur du corps et `q` la longueur de la queue du poisson.
`t=9`
`c=t+q=9+q` (1)
`q=t+c/2=9+c/2` (2)
En ajoutant (1) dans (2):
`c+9+c/2=9+q+q`
`iff 3/2c=2q`
`iff c=4/3q` (3)
(3) dans (1):
`4/3q=9+q`
`iff q=27`
`=> c=36`
Donc la longueuer totale du poisson est de `9+36+27=72` centimètres.
`t=9`
`c=t+q=9+q` (1)
`q=t+c/2=9+c/2` (2)
En ajoutant (1) dans (2):
`c+9+c/2=9+q+q`
`iff 3/2c=2q`
`iff c=4/3q` (3)
(3) dans (1):
`4/3q=9+q`
`iff q=27`
`=> c=36`
Donc la longueuer totale du poisson est de `9+36+27=72` centimètres.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Question 24
Question 24
Le graphe B) est celui qui représente la longueur des cheveux en fonction du temps. Les cheveux croissent en vitesse constante. Après un certain temps, la personne va chez le coiffeur qui coupe les cheveux à leur longueur initiale, laquelle est évidemment plus petite. Après les cheveux continuent à croître et la routine recommence.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Question 22
Question 22
Soit `A(C)` et `A(D)` l'aire des surfaces des cubes C et D respectivement et `c` et `d` les longueurs des arrêtes. Donc `A(C)=6c^2` et:
`A(D)=6*d^2`
`=16*6c^2` (car A(D)=16A(C))
`=6*(4c)^2`
Donc d est le quadruple de c. Ainsi:
`Volume(D)=(4c)^3`
`=64c^3`
Il faut remplir 64 fois plus de liquide pour D que pour C.
`A(D)=6*d^2`
`=16*6c^2` (car A(D)=16A(C))
`=6*(4c)^2`
Donc d est le quadruple de c. Ainsi:
`Volume(D)=(4c)^3`
`=64c^3`
Il faut remplir 64 fois plus de liquide pour D que pour C.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Question 21
Question 21
`((4^4*3^16)/(9^8*2^7))^6`
`=((2^8*3^16)/(3^16*2^7))^6`
`=2^6`
`=64`
La réponse E) est juste.
`=((2^8*3^16)/(3^16*2^7))^6`
`=2^6`
`=64`
La réponse E) est juste.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Question 20
Question 20
65% de 300:
`65/100*300=195`
Hypathie les coupe en quatre ce qui donne `4*195=780` morceaux de chocolat. En tout elle a:
`780+(300-195)=885` morceaux de chocolat. Donc elle a:
`885-300=585` morceaux en plus. Réponse C) est correcte.
`65/100*300=195`
Hypathie les coupe en quatre ce qui donne `4*195=780` morceaux de chocolat. En tout elle a:
`780+(300-195)=885` morceaux de chocolat. Donc elle a:
`885-300=585` morceaux en plus. Réponse C) est correcte.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Question 19
Question 19
`B=2A`
`C=3B=3*2A=6A`
`D=4C=4*6A=24A`
`E=5D=5*24A=120A`
`E-A=833`
`iff 120A-A=833`
`iff A=7`
Ainsi: `B=2*7=14`
`C=6*7=42`
`D=24*7=168`
`E=120*7=840`
`B, C, D` et `E` sont paires.
`C=3B=3*2A=6A`
`D=4C=4*6A=24A`
`E=5D=5*24A=120A`
`E-A=833`
`iff 120A-A=833`
`iff A=7`
Ainsi: `B=2*7=14`
`C=6*7=42`
`D=24*7=168`
`E=120*7=840`
`B, C, D` et `E` sont paires.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Question 18
Question 18
Les aiguilles forment un angle de 180 degrées à (environ):
0h31
1h37
2h43
3h49
4h55
6h
7h05
8h10
9h15
10h20
11h25
donc 11 fois. En 24 heures, les aiguilles de l'horloge font `2*11=22` fois un angle de 180 degrées. C) est juste.
0h31
1h37
2h43
3h49
4h55
6h
7h05
8h10
9h15
10h20
11h25
donc 11 fois. En 24 heures, les aiguilles de l'horloge font `2*11=22` fois un angle de 180 degrées. C) est juste.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Question 17
Question 17
Soit `AB=BC=CD=DA=1` et `DE=1/2`
`Aire(EDC)=(DE*CD)/2`
`=(1/2*1)/2`
`=1/4`
`Aire(BCD)=(CD*BC)/2`
`=(1*1)/2`
`=1/2`
Le rapport `(Aire(EDC))/(Aire(BCD))` est de:
`(1/4)/(1/2)=1/2`
La réponse A) est correcte.
`Aire(EDC)=(DE*CD)/2`
`=(1/2*1)/2`
`=1/4`
`Aire(BCD)=(CD*BC)/2`
`=(1*1)/2`
`=1/2`
Le rapport `(Aire(EDC))/(Aire(BCD))` est de:
`(1/4)/(1/2)=1/2`
La réponse A) est correcte.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Question 16
Question 16
D'après le thèorème de Pythagore:
`CX^2=CG^2+GH^2+HX^2`
`iff CX=sqrt(1^2+1^2+0,5^2)
`=sqrt(2,25)`
`=1,5`
`=3/2`
C) est juste.
`CX^2=CG^2+GH^2+HX^2`
`iff CX=sqrt(1^2+1^2+0,5^2)
`=sqrt(2,25)`
`=1,5`
`=3/2`
C) est juste.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Bravo
Bravo
Très bon travail jusqu'à présent! 
Juste un petit détail t' est échappé: la titre de ta réponse à la question 23 est différent des autres...
Encore félicitations pour ton score parfait aux éliminatoires et bonne chance pour demain dans la demi-finale!
Juste un petit détail t' est échappé: la titre de ta réponse à la question 23 est différent des autres...
Encore félicitations pour ton score parfait aux éliminatoires et bonne chance pour demain dans la demi-finale!

carole- Expert

- Messages : 181
Date d'inscription : 11/05/2010
Age : 31
 Bravo !
Bravo !
Je suis tout à fait d'accord avec Carole !
Beau travail jusqu'ici !
J'attends la suite avec impatience !
Peut-être après la période des composition ??
Cordialement G. Lorang
Beau travail jusqu'ici !
J'attends la suite avec impatience !
Peut-être après la période des composition ??
Cordialement G. Lorang
 Question 15
Question 15
L'enfant doit prendre `10*0,05 mL=0,5mL`.
`50mm^3=0,05mL`
`100mm^3=0,1mL`
`200mm^3=0,2mL`
Donc l'enfant prendre une quantité de 2 cuillères de `200mm^3` et 1 cuillère de `100mm^3` (2*0,2mL+0,1mL=0,5mL). E) est correcte.
`50mm^3=0,05mL`
`100mm^3=0,1mL`
`200mm^3=0,2mL`
Donc l'enfant prendre une quantité de 2 cuillères de `200mm^3` et 1 cuillère de `100mm^3` (2*0,2mL+0,1mL=0,5mL). E) est correcte.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Question 14
Question 14
Après la visite du client à Mons, le représentant a 5 choix (Bruxelles, Charleroi, Namur, Liège et Bastogne) pour avancer son trajet. Après la deuxième visite, il ya 4 possibilités pour la troisième visite et ainsi de suite. Donc il a `5*4*3*2*1=120` possibilités pour programmer la tournée.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Question 13
Question 13
Nombre de cubes: `1^2+3^2+5^2+7^2+5^2+3^2+1^2=119`

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Question 12
Question 12
On a: `x^4-y^4=(x^2-y^2)(x^2+y^2)`
Aisni: `((x^2-y^2)(x^2+y^2))/(x^2-y^2)=x^2+y^2`
`=16/4=4`
Réponse B) est juste.
Aisni: `((x^2-y^2)(x^2+y^2))/(x^2-y^2)=x^2+y^2`
`=16/4=4`
Réponse B) est juste.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Question 11
Question 11
La moitié de la grande diagonale mesure 8cm. Comme on connait la longueur du côté, on peut calculer la moitié de la petite diagonale à l'aide de Pythagore.
`10^2=8^2+(d_p/2)^2`
`iff d_p=sqrt(4(100-64))`
`=12`
Aire du losange: `Aire=1/2*d_p*d_g =96 (cm^2)`
D) est correcte.
`10^2=8^2+(d_p/2)^2`
`iff d_p=sqrt(4(100-64))`
`=12`
Aire du losange: `Aire=1/2*d_p*d_g =96 (cm^2)`
D) est correcte.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
 Question 10
Question 10
On peut déduire que le chiffre de centaines est six fois plus grand que le chiffre des unités. Là, il n'y a qu'une seule possibilité: 6 pour le chiffre de centaines et 1 pour le chiffre des unités. Ainsi le chiffre des dizaines est 3 est le nombre cherché est 631.

Alain- Pro

- Messages : 70
Date d'inscription : 25/03/2011
Age : 27
Page 1 sur 2 • 1, 2 
 Sujets similaires
Sujets similaires» OMB Eliminatoires 2013
» OMB-Midi Eliminatoires 2012
» OMB- Eliminatoires 2012
» Eliminatoires 2011 OMB-Mini
» Eliminatoires 2011 OMB-Midi
» OMB-Midi Eliminatoires 2012
» OMB- Eliminatoires 2012
» Eliminatoires 2011 OMB-Mini
» Eliminatoires 2011 OMB-Midi
Page 1 sur 2
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum|
|
|

