OMB-Maxi Test d'entraînement 2011/2012
2 participants
Page 1 sur 1
 Re: OMB-Maxi Test d'entraînement 2011/2012
Re: OMB-Maxi Test d'entraînement 2011/2012
Je pense qu' il y a déjà quelques questions résolues dans la rubrique MIDI, à savoir la question 3, peut-être quelques autres...
Question 1:
Si on veut relier les 2005 maisons telles qu' elles soient reliés tous aux autres (en passant par d' autres) on a besoin de au moins 2004 câbles. 1003 est faux car alors le maisons sont reliées par couple de deux, mais elles ne peuvent recevoir des messages des autres. Voir figure avec 7 maisons (points verts) et les câbles (en rouge):

la bonne réponse est donc B: 2004
Question 2:
Après avoir frappé le clou une première fois il s' enfonce de `3*1/3=1` cm dans le mur. Puis on le frappe une deuxième fois et il reste `2-2*1/3=4/3` cm hors du mur. Après le troisème coup il ne reste plus que `4/3*2/3=8/9<1` cm hors du mur. Donc la bonne réponse est C:3.
Question 4:
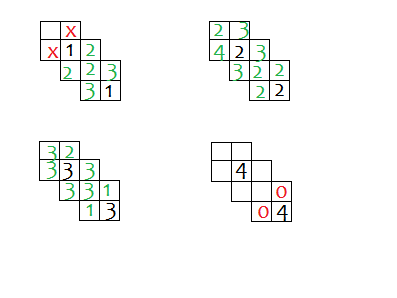
Les nombre 2 et 3 sont corrects (en noir). Donc la réponse B est correcte!
(J' ai toujours commencé en bas à droite)
Question 1:
Si on veut relier les 2005 maisons telles qu' elles soient reliés tous aux autres (en passant par d' autres) on a besoin de au moins 2004 câbles. 1003 est faux car alors le maisons sont reliées par couple de deux, mais elles ne peuvent recevoir des messages des autres. Voir figure avec 7 maisons (points verts) et les câbles (en rouge):

la bonne réponse est donc B: 2004
Question 2:
Après avoir frappé le clou une première fois il s' enfonce de `3*1/3=1` cm dans le mur. Puis on le frappe une deuxième fois et il reste `2-2*1/3=4/3` cm hors du mur. Après le troisème coup il ne reste plus que `4/3*2/3=8/9<1` cm hors du mur. Donc la bonne réponse est C:3.
Question 4:

Les nombre 2 et 3 sont corrects (en noir). Donc la réponse B est correcte!
(J' ai toujours commencé en bas à droite)

carole- Expert

- Messages : 181
Date d'inscription : 11/05/2010
Age : 31
 Re: OMB-Maxi Test d'entraînement 2011/2012
Re: OMB-Maxi Test d'entraînement 2011/2012
Question 5:
`5n` est pair si n est pair!
`n^2+1` est pair si `n^2` (donc n) est impair!
`n^2` est pair si n est pair!
`n^2+n+1` est toujours impair (ou bien somme de 2 nombres pairs et un entier impair, ou bien somme des 3 entiers impairs)
`3n^2-5n` est toujours pair!
Donc la réponse B:1 est correcte!
Question 6:

L' aire du triangle ABC est un nombre rationnel, donc D est correcte!
Explication: Aire(ABC)=Aire(AC'B'A')-Aire(AC'B)-Aire(BA'C)-Aire(AB'C)
Or l' aire de ACB'C' est un entier, et celles de ABC', A'BC et AB'C sont des nombres rationnels.
Donc l' aire de ABC est bien rationnelle!
Question 7:
Le bon graphe est A, car la pente doit être positive (+-5/9), le graphe doit passer par (0,32) et le point (-10,0) ne peut appartenir au graphe!
Question 8:
si n=2: `2^2+2+1=7
si n=3: `3^2+3+1=13
si n=4: `4^2+4+1=21
si n=5: `5^2+5+1=31=27+4=3^3+2^2
Donc la réponse correcte vaut 31!
`5n` est pair si n est pair!
`n^2+1` est pair si `n^2` (donc n) est impair!
`n^2` est pair si n est pair!
`n^2+n+1` est toujours impair (ou bien somme de 2 nombres pairs et un entier impair, ou bien somme des 3 entiers impairs)
`3n^2-5n` est toujours pair!
Donc la réponse B:1 est correcte!
Question 6:

L' aire du triangle ABC est un nombre rationnel, donc D est correcte!
Explication: Aire(ABC)=Aire(AC'B'A')-Aire(AC'B)-Aire(BA'C)-Aire(AB'C)
Or l' aire de ACB'C' est un entier, et celles de ABC', A'BC et AB'C sont des nombres rationnels.
Donc l' aire de ABC est bien rationnelle!
Question 7:
Le bon graphe est A, car la pente doit être positive (+-5/9), le graphe doit passer par (0,32) et le point (-10,0) ne peut appartenir au graphe!
Question 8:
si n=2: `2^2+2+1=7
si n=3: `3^2+3+1=13
si n=4: `4^2+4+1=21
si n=5: `5^2+5+1=31=27+4=3^3+2^2
Donc la réponse correcte vaut 31!

carole- Expert

- Messages : 181
Date d'inscription : 11/05/2010
Age : 31
 Re: OMB-Maxi Test d'entraînement 2011/2012
Re: OMB-Maxi Test d'entraînement 2011/2012
Question 9:
`(x+1/x)^2=5
`iff x+1/x=sqrt(5)` car `x` est positif
`iff x^2+1/x^2=5-2=3
`(x^2+1/x^2)(x+1/x)=3sqrt(5)
`iff x^3+x+1/x+1/x^3=3sqrt(5)
`iff x^3+sqrt(5)+1/x^3=3 sqrt(5)
`iff x^3+1/x^3=2sqrt(5)
Donc la réponse C est correcte!
Question 10:
Il existe 8 couples:
si x=+-1, alors y=+-2 (4 possibilités)
si x=+-2, alors y=+-1 (4 possibilités)
On ne peut pas avoir d' autres couples car plus les carrés deviennent grand, plus leur différece devient grande!
(Je ne traite pas tous les cas ici...)
Question 11:
La bonne réponse est C!
Le point (3,3) doit appartenir au graphe, ce qui est le cas pour B et C.
Or, le point (0,-6) doit appartenir au graphe de B, ce qui n' est pas le cas!
Question 13:
La réponse D est correcte, car:
`(x+1)^3+4=x^3+3x^2+3x+5=y
(On a effectué une translation de `vec(u)=-vec(i)+4vec(j)` de la courbe `y=x^3` qui admet un centre de symmétrie en `(0,0)`.)
`(x+1/x)^2=5
`iff x+1/x=sqrt(5)` car `x` est positif
`iff x^2+1/x^2=5-2=3
`(x^2+1/x^2)(x+1/x)=3sqrt(5)
`iff x^3+x+1/x+1/x^3=3sqrt(5)
`iff x^3+sqrt(5)+1/x^3=3 sqrt(5)
`iff x^3+1/x^3=2sqrt(5)
Donc la réponse C est correcte!
Question 10:
Il existe 8 couples:
si x=+-1, alors y=+-2 (4 possibilités)
si x=+-2, alors y=+-1 (4 possibilités)
On ne peut pas avoir d' autres couples car plus les carrés deviennent grand, plus leur différece devient grande!
(Je ne traite pas tous les cas ici...)
Question 11:
La bonne réponse est C!
Le point (3,3) doit appartenir au graphe, ce qui est le cas pour B et C.
Or, le point (0,-6) doit appartenir au graphe de B, ce qui n' est pas le cas!
Question 13:
La réponse D est correcte, car:
`(x+1)^3+4=x^3+3x^2+3x+5=y
(On a effectué une translation de `vec(u)=-vec(i)+4vec(j)` de la courbe `y=x^3` qui admet un centre de symmétrie en `(0,0)`.)

carole- Expert

- Messages : 181
Date d'inscription : 11/05/2010
Age : 31
 Re: OMB-Maxi Test d'entraînement 2011/2012
Re: OMB-Maxi Test d'entraînement 2011/2012
Question 15:
Un nombre est à la fois carré et cube d' un autre s' il s' écrit sous la forme `p=q^6=(q^2)^3=(q^3)^2`.
Or il existe 4 tels nombres `p<10^3`:
`0^6=0
`1^6=1
`2^6=64
`3^6=729
Question 17:
Le bon rapport est 4/1, donc C est correcte!
Calculs: (x est la longeur du segment parallèle entre les deux bases initiales)
Périmètre du trapèze d' "en haut":
`6+x+4/5*12+4/5*8=22+x
Périmètre du trapèze d' en bas:
`18+x+1/5*12+1/5*8=22+x
Question 18:
La réponse E est correcte:
par exemple la fonction: `x->|x|` est continue sur `RR`, mais non dérivable en `x=0`!
Un nombre est à la fois carré et cube d' un autre s' il s' écrit sous la forme `p=q^6=(q^2)^3=(q^3)^2`.
Or il existe 4 tels nombres `p<10^3`:
`0^6=0
`1^6=1
`2^6=64
`3^6=729
Question 17:
Le bon rapport est 4/1, donc C est correcte!
Calculs: (x est la longeur du segment parallèle entre les deux bases initiales)
Périmètre du trapèze d' "en haut":
`6+x+4/5*12+4/5*8=22+x
Périmètre du trapèze d' en bas:
`18+x+1/5*12+1/5*8=22+x
Question 18:
La réponse E est correcte:
par exemple la fonction: `x->|x|` est continue sur `RR`, mais non dérivable en `x=0`!

carole- Expert

- Messages : 181
Date d'inscription : 11/05/2010
Age : 31
 Remarques :
Remarques :
Question 1 : En notant les maisons par `m_1` , `m_2`, `m_3`, ... `m_2005`, il suffit de réaliser une connection linéaire `m_1 -> m_2 ->m_3 ->...->m_2004 ->m_2005`, où les flèches symbolisent les câbles. Il y a donc 2004 câbles au minimum à installer. Bien sûr, en pratique, on essaye de minimiser la longeur totale des câbles, et pas le nombre de câbles.
Question 2 : On peut donner une formule générale. Soit `u_n` la longueur de clou qui dépasse du mur après `n` coups. `u_0=3` et `u_n=u_(n-1)*2/3`. Donc `(u_n)` est une suite géométrique de 1er terme 3 et de raison 2/3. On a donc : `u_n=3*(2/3)^n`. Comme Carole précise, `u_3=8/9` est la première valeur <1.$
Question 6 : On peut préciser que la réponse est toujours de la forme `n` ou `n/2` où `n` est un entier.
Question 10 : L'équation peut s'écrire : `(x-y)(x+y)=+-3`, donc `x-y=+-1` et `x+y=+-3` ou `x-y=+-3` et `x+y=+-1`. En additionnant membre par membre les deux équations, on a : `2x=+-2` ou `2x=+-4`, càd `x=+-1` ou `x=+-2`. A partir de là, on trouve rapidement les couples solution.
Question 17 : Soit `r` le rapport cherché. La parallèle coupe les côtés de longueurs 8 et 12 respectivement dans le même rapport, d'après le théorème de Thalès. Faites une figure ! Si on appelle `a` et `b` les longeurs des deux segments obtenus en coupant par exemple le côté de longeur 8, on a :
`a+b=8` et `a/b=r`. En résolvant ce système, on trouve aisément :
`b=8/(1+r)` et `a=(8r)/(1+r)`.
De même, on détermine en fonction de `r` les longeurs des deux segments sur les deux autres côtés.
D'où l'équation qui traduit l'égalité des périmètres :
`6+x+(8r)/(1+r)+(12r)/(1+r)=x+18+8/(1+r)+(12)/(1+r)`
`iff (20r)/(1+r)-(20)/(1+r)=12
`iff (20(r-1))/(r+1)=12
`iff (r-1)/(r+1)=3/5
`iff 5r-5=3r+3
`iff r=4
Question 19 :
On calcule `A_0A_1` à l'aide du théorème de Pythagore : `A_0A_1=sqrt(1/2+1/4)=sqrt(3)/2`
En appliquant le théorème de Thalès, il est facile de voir que `A_1A_2=1/2A_0A_1`, `A_2A_3=1/2A_1A_2`, etc.
Donc, la longueur de la ligne brisée est :
`A_0A_1+1/2A_0A_1+1/4A_0A_1+1/8A_0A_1+...`
`=A_0A_1(1+1/2+1/4+1/8+...)
`=A_0A_1*1/(1-1/2)` (Formule : `1+r+r^2+r^3+...=1/(1-r)`, si `-1<r<1`)
`=sqrt(3)/2*2=sqrt(3)`
Donc la réponse B est correcte.
Question 2 : On peut donner une formule générale. Soit `u_n` la longueur de clou qui dépasse du mur après `n` coups. `u_0=3` et `u_n=u_(n-1)*2/3`. Donc `(u_n)` est une suite géométrique de 1er terme 3 et de raison 2/3. On a donc : `u_n=3*(2/3)^n`. Comme Carole précise, `u_3=8/9` est la première valeur <1.$
Question 6 : On peut préciser que la réponse est toujours de la forme `n` ou `n/2` où `n` est un entier.
Question 10 : L'équation peut s'écrire : `(x-y)(x+y)=+-3`, donc `x-y=+-1` et `x+y=+-3` ou `x-y=+-3` et `x+y=+-1`. En additionnant membre par membre les deux équations, on a : `2x=+-2` ou `2x=+-4`, càd `x=+-1` ou `x=+-2`. A partir de là, on trouve rapidement les couples solution.
Question 17 : Soit `r` le rapport cherché. La parallèle coupe les côtés de longueurs 8 et 12 respectivement dans le même rapport, d'après le théorème de Thalès. Faites une figure ! Si on appelle `a` et `b` les longeurs des deux segments obtenus en coupant par exemple le côté de longeur 8, on a :
`a+b=8` et `a/b=r`. En résolvant ce système, on trouve aisément :
`b=8/(1+r)` et `a=(8r)/(1+r)`.
De même, on détermine en fonction de `r` les longeurs des deux segments sur les deux autres côtés.
D'où l'équation qui traduit l'égalité des périmètres :
`6+x+(8r)/(1+r)+(12r)/(1+r)=x+18+8/(1+r)+(12)/(1+r)`
`iff (20r)/(1+r)-(20)/(1+r)=12
`iff (20(r-1))/(r+1)=12
`iff (r-1)/(r+1)=3/5
`iff 5r-5=3r+3
`iff r=4
Question 19 :
On calcule `A_0A_1` à l'aide du théorème de Pythagore : `A_0A_1=sqrt(1/2+1/4)=sqrt(3)/2`
En appliquant le théorème de Thalès, il est facile de voir que `A_1A_2=1/2A_0A_1`, `A_2A_3=1/2A_1A_2`, etc.
Donc, la longueur de la ligne brisée est :
`A_0A_1+1/2A_0A_1+1/4A_0A_1+1/8A_0A_1+...`
`=A_0A_1(1+1/2+1/4+1/8+...)
`=A_0A_1*1/(1-1/2)` (Formule : `1+r+r^2+r^3+...=1/(1-r)`, si `-1<r<1`)
`=sqrt(3)/2*2=sqrt(3)`
Donc la réponse B est correcte.
 Sujets similaires
Sujets similaires» OMB-Maxi Test d'entraînement 2012/2013
» Test d'entraînement OMB MAXI 2010/2011
» OMB-Maxi Demi-finales 2011
» OMB-Mini Test d'entraînement 2011/2012
» OMB-Maxi Finale 2012
» Test d'entraînement OMB MAXI 2010/2011
» OMB-Maxi Demi-finales 2011
» OMB-Mini Test d'entraînement 2011/2012
» OMB-Maxi Finale 2012
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum|
|
|




