Un problème de courbure (à préparer pour la compo ...)
3 participants
Page 1 sur 1
 Un problème de courbure (à préparer pour la compo ...)
Un problème de courbure (à préparer pour la compo ...)
Une route est représentée par l'arc de cercle `AB` avec `A(-7,0)` et `B(2,3)`. Le centre de l'arc est `I(-2,0)`. (Voir figure.) La route doit être prolongée au point B(2,3) par une nouvelle route représentée par le graphe d'un polynôme `g`. Déterminer ce polynôme `g` de façon à ce que 1) le passage de l'une des routes vers l'autre se fasse "sans heurts", c.-à-d. pour que la courbure de la route soit continue en `B` et 2) le graphe de `g` passe par le point `C(6,6)`. On demande de déterminer `g` de degré minimal.
Figure :
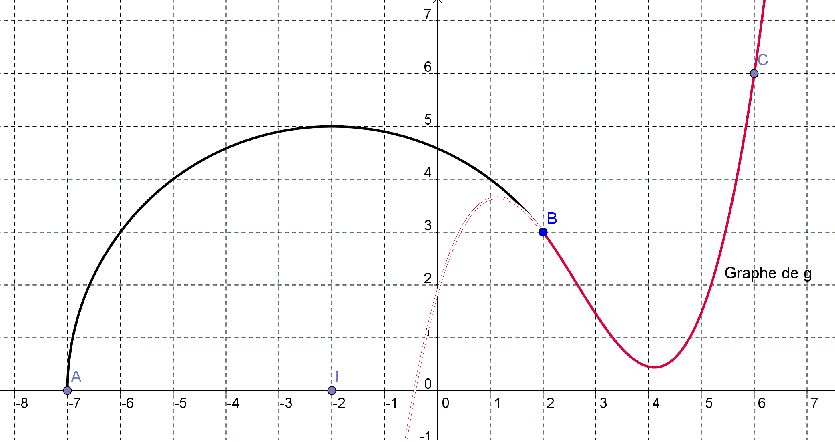
Figure :

 réponse:
réponse:
On a une fonction de cercle : `g(x)=sqrt(5^2-(x+2)^2)`
(ne pas prendre la lettre 'c' , comme fonction, afin d'éviter des conflict de variables =
=  )
)
On cherche une fonction f, de degré minimal remplissant les conditions suivantes:
`{(f(2)=3text( c'est le point d'intersection entre le cercle c et la fonction f,cherchée)),(f'(2)=g'(2)text( la pente de Gf est la même que celle du cercle au point d'intersection d'abscisse 2)),(k_(f)(2)=-1/5text ( où -1/5= courbure du cercle c, de rayon 5) rarr text(cette condition peut aussi s'écrire:) f''(2) =g''(2)),(f(6)=6text( Gf passe par le point c(6;6)):}`
Comme il y a 4 conditions à remplir, le polynome cherché doit être du 3 degré(au moins) et ce présente sous la forme: `f(x)= a*x^3+b*x^2+c*x+d)` où les inconnues cherchées sont a, b, c et d.
N'oubliez pas de définir kf(x)comme la courbure de f au point d'abscisse x !!
En solvant le système d'equations à conditions nécessaires et suffisantes, à l'aide de la V200 , on trouve :
`f(x) = 425/1728*x^3-1675/864*x^2+1499/432*x+133/72`

p.S. hun leider variablen bessi vertosch and nimm vun dn fonct. net grad wei am enoncé xD

(ne pas prendre la lettre 'c' , comme fonction, afin d'éviter des conflict de variables
 )
) On cherche une fonction f, de degré minimal remplissant les conditions suivantes:
`{(f(2)=3text( c'est le point d'intersection entre le cercle c et la fonction f,cherchée)),(f'(2)=g'(2)text( la pente de Gf est la même que celle du cercle au point d'intersection d'abscisse 2)),(k_(f)(2)=-1/5text ( où -1/5= courbure du cercle c, de rayon 5) rarr text(cette condition peut aussi s'écrire:) f''(2) =g''(2)),(f(6)=6text( Gf passe par le point c(6;6)):}`
Comme il y a 4 conditions à remplir, le polynome cherché doit être du 3 degré(au moins) et ce présente sous la forme: `f(x)= a*x^3+b*x^2+c*x+d)` où les inconnues cherchées sont a, b, c et d.
N'oubliez pas de définir kf(x)comme la courbure de f au point d'abscisse x !!
En solvant le système d'equations à conditions nécessaires et suffisantes, à l'aide de la V200 , on trouve :
`f(x) = 425/1728*x^3-1675/864*x^2+1499/432*x+133/72`

p.S. hun leider variablen bessi vertosch and nimm vun dn fonct. net grad wei am enoncé xD

Dernière édition par Tom le Jeu 13 Mai - 20:56, édité 22 fois
 Wiesou sou komplizeiert?
Wiesou sou komplizeiert?
Tom ej wees io net opste dem Herr Lorang dei lescht Stonn nogelaustert hues,
mee hien hued ons klib an kloer ercklärt dass dei heiten condition: kf(2)=-1/5
och einfach duerch f''(2)=g''(2) keins ersätzen, wiesou dat sou as hun ma opgeschriwn .
.
Tom you got pwnd =D gg
mee hien hued ons klib an kloer ercklärt dass dei heiten condition: kf(2)=-1/5
och einfach duerch f''(2)=g''(2) keins ersätzen, wiesou dat sou as hun ma opgeschriwn
Tom you got pwnd =D gg

Rage_Quitsch- New

- Messages : 3
Date d'inscription : 11/05/2010
Age : 33
Localisation : Planet Earth =)
 wanns de mengs..
wanns de mengs..
jo d'ass jo schein xd.. du häss jo och keinten d'leisung posten xD
why emmer kritik? ech änneren et ...dengetwegen.
why emmer kritik? ech änneren et ...dengetwegen.
 1337
1337
Ej wollt dej halt nemmen drop hiweisen, sou kannste während der Prüfung
vill Zeit spueren . Mee du brauchs deng Leisung lo doweings eindeutej net
. Mee du brauchs deng Leisung lo doweings eindeutej net
ze änneren, wat schon nees ze vill Arbescht as.
Dei Leit dei et aanejt wellen machen gesin io an mengem post wat se änneren
mussen...
(An Kritik as emmer konstruktiv =P)
vill Zeit spueren
ze änneren, wat schon nees ze vill Arbescht as.
Dei Leit dei et aanejt wellen machen gesin io an mengem post wat se änneren
mussen...
(An Kritik as emmer konstruktiv =P)

Rage_Quitsch- New

- Messages : 3
Date d'inscription : 11/05/2010
Age : 33
Localisation : Planet Earth =)
 Sujets similaires
Sujets similaires» OMB-Maxi Finale 2011
» THIRD BENELUX MATHEMATICAL OLYMPIAD : BxMO 2011
» OMB-Maxi Finale 2012
» European Girls' Mathematical Olympiad (EGMO) 2012 :
» Des probléme en math ??
» THIRD BENELUX MATHEMATICAL OLYMPIAD : BxMO 2011
» OMB-Maxi Finale 2012
» European Girls' Mathematical Olympiad (EGMO) 2012 :
» Des probléme en math ??
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum|
|
|

